/*
기술 통계학(descriptive statistics)는 측정이나 실험에서 수집한 자료의 정리, 표현, 요약, 해석 등을 통해 자료의 특성을 규명하는 통계적 방법이다.
한 표본의 조사로부터 전체 집단의 현상을 추리하는 통계학. 확률론 따위의 방법을 쓴다.
그룹화된 데이터: 도수 분포
Sturge's rule: 데이터가 N개일 때, histogram에서 breaks의 수를 k = 1 + 3.322 * log_10(N)로 하면 좋다. 라는 뜻.
N이 만약 500이라면, 1+3.322 * log_10(500) = 1 + 3.322*2.69897 = 9.965978
9.97.. 정도이기 때문에 breaks를 10개로 설정하면 보기 좋다.
(Sturge 이건 옛날의 흔적..?)
R코드는 다음과 같다.
hist(birth$gestwks, breaks=1+3.322*log(500,10))
(기술통계학 - Descriptive stat)
Central tendency: 중심 성향
Population mean: 모평균
Sample mean: 표준평균
표본으로부터 계산된 기술통계량을 통계량(statistics)이라고 하고, 모집단으로부터 얻어진 기술 통계량은 모수 (parameter)라 한다.
산술평균의 특징.
모든 데이터는 오직 하나의 산술평균만을 갖는다. (유일성)
산술평균은 그 의미를 이해하기 쉬우며 계산이 간단하다 (간결성).
산술평균은 모든 데이터를 이용하여 계산하기 때문에 개별 값에 영향을 받는다. (sensitive to outlier)
Median은 outlier에 대해 robust 하다 (둔감하다).
Mean은 outlier에 대해 sensitive 하다 (민감하다).
왜도: Skewness
얼마나 자료가 한쪽으로 치우쳤느냐?
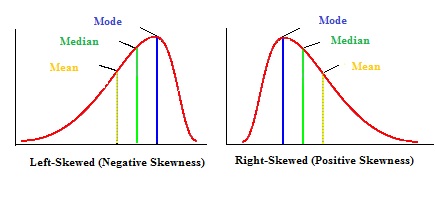
왼쪽으로 꼬리가 길다 = left skewed = 자료가 오른쪽으로 치우쳤다
오른쪽으로 꼬리가 길다 = right skewed = 자료가 왼쪽으로 치우쳤다.
skewed가 한국어로 치우쳤다고 해석하게되면 반대로 해석하게 될 수 있으므로, 주의!
left skewed는 왼쪽으로 꼬리가 길기 때문에, mean < median
right skewed는 오른쪽으로 꼬리가 길기 때문에, mean > median
income 같은 경우, median을 구해야 상위50%, 하위 50%의 중심을 알 수 있음.
mean을 구해버리면 실제 중간 사람들의 income을 반영하지 않음,.
표본분산: 편차^2 / (n-1)
모분산: 편차^2/n
변동계수: Coefficient of variation
C.V. : 표준편차 / 평균 * 100%
평균이 커질수록 표준편차도 따라서 커지는 경향이 있다.
따라서 표준편차를 평균으로 나눠주는 변동계수가 유용할 경우가 있음.
> summary(rnorm(n=50, mean=100, sd=10))
Min. 1st Qu. Median Mean 3rd Qu. Max.
82.76 92.40 103.80 102.10 109.40 125.50
사분위 범위 (Interquartile range: IQR) = Q3 - Q1
이것도 좀 robust 한 값..
첨도: 뾰족한지 평평한지를 나타내는 척도
Kurtosis
'Programing > R- programming' 카테고리의 다른 글
| R에서 ROC curve 그리기 (0) | 2018.03.19 |
|---|---|
| R을 이용해서 Image augmentation 하기. (0) | 2017.10.03 |
| R notebooks Markdown release! (0) | 2016.11.23 |
| Expectation–maximization과 R을 이용한 구현 (0) | 2016.11.09 |
| WARNING: Only g++ version 4.6 or greater can be used with RcppArmadillo (0) | 2016.06.15 |